|
|
LAMONT-DOHERTY EARTH OBSERVATORY THE EARTH INSTITUTE AT COLUMBIA UNIVERSITY |
||
| Abrupt Climate Change | ||
| LDEO | ||
| Home | ||
| Divisions | ||
| LDEO Search | ||
| Abrupt CC | ||
| Home | ||
| Q&A | ||
| Contacts | ||
| Research | ||
| Links |
back to Q&A The Earth's climate: a non-linear dynamical system
Dynamics is the branch of mechanics that is concerned with the effects of forces on the motion of objects (from Wikipedia). More generally, it could be defined as the study of changes, therefore applying to anything that does not stay constant. This is virtually everything. Climate is one such example.
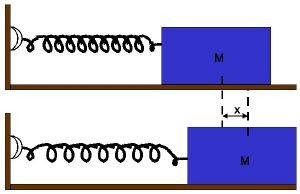
Even if you ignore everything about quantum physics and relativity, you probably know that the world is more complicated than even quirky physicists would like it to be. In fact, "complex" behavior (what quirky physicists call "interesting") can occur in systems than follow the deceitfully simple laws of classical mechanics, which have been set out in1687 by Isaac Newton. In mechanical systems, such as the ocean and the atmosphere, the richness of behavior stems from a mathematical property called nonlinearity, which can lead to chaos. Essentially, a linear system is one where doubling the perturbation doubles the response. For example, if I have spring and I pull on it slightly (a small distance x on the figure below), it will undergo oscillations that are nice and regular.
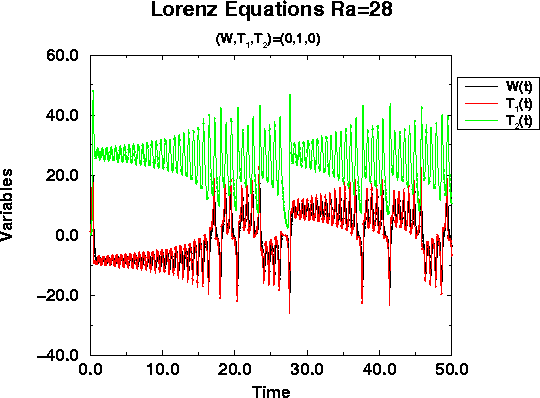
Figure 1: a simple linear system:{spring + mass} If I pull on it twice as much (2x), but still not quite like a brute, it will display oscillations of the same period but with an amplitude that is twice as large ; these are nice, linear oscillations. Although this seems very intuitive to most of us, it is almost always an idealization: if I now pull on it like a brute, the spring might outstretch irreversibly. It will then not be able to behave like an elastic as before: the system is now non-linear. It might oscillate a bit, but not as simply as before. Unfortunately most natural systems are not nice and linear. Their understanding therefore requires the study of nonlinear dynamics. For an excellent tutorial on dynamical systems and chaos, go to Marc Spiegelman's page. If you think you know enough already, let us turn to an example relevant for climate dynamics, Lorenz's model. This model is extremely famous and it explained is great detail in many places ( here for pretty pictures, here for an illuminating tutorial, or here again). It was set out by Edward Lorenz, and MIT meteorologist, in a pioneering paper called "Deterministic non-periodic flow" (1963), more commonly known by its nickname, the Butterfly effect. Lorenz's model is a very simplified model of atmospheric convection, which is a system where temperature and fluid motion interact very non-linearly: one feedbacks on the other. If the system is described by 3 variables W, T1 and T2 (see here for what they mean), then for a sufficiently high parameter (named the Rayleigh number), the system exhibits oscillations that are not periodic, hence hard to predict.
Figure 2: A very complex non-linear system, with only 3 variables. These are the solutions of the Lorenz system for a Rayleigh number of 28. W is the amplitude of the vertical velocity and T1 and T2 govern horizontal and vertical temperature patterns in the model. (credit: Marc Spiegelman) Indeed, just looking at the red curve, one sees the oscillations growing in time, but still hanging about -9 or so. Between t=28 and t=36 (roughly), the system is oscillating about +9. These correspond to centers in the phase space of the system. The associated phase portrait is called a "strange attractor" because it does look a little strange... (it has a non-integer dimension). The fact that it can go erratically, and often abruptly, from the neighborhood of one center to the other is the essence of a chaotic behavior. This property manifests itself as a sensitivity to initial conditions : any small imprecision in the knowledge of one parameter will make it impossible to know where the system is going to be after some finite time: in other words, it is unpredictable. Bad news for weather forecasters, but they are used to it now. It is possible that the climate of the Earth behaves this way. |
|
|

NGDC |
Modeling Observations Paleoclimate |

NAS Report on Abrupt Climate Change |

LDEO CORC/ARCHES Project |
The trigger for the Younger Dryas |

Cultural responses to climate change |

Solar influence on climate change |
LDEO home | search | webmaster | site map | terms-of-use | support LDEO
Copyright © 2003 by The Trustees of Columbia University in the City of New York, Lamont-Doherty Earth Observatory.
All rights reserved.