Discussion

There are several aspects of these observations which at first appear contradictory. In particular, onshore and westward flow in the BBL is not consistent with Ekman dynamics. This apparent contradiction is resolved in non-linear model calculations by Chapman and Lentz (1994) where they consider frontogenesis on the shelf driven by a coastal buoyancy source. The offshore migration of the front is arrested when in the BBL offshore flow of buoyant shelf water converges with an onshore flow underneath the frontal boundary. The cross-shelf convergence zone in the BBL is at the shoreward side of the frontal boundary. The thermal wind shear in response to the increased cross-shelf density gradient reverses the alongshore flow at the foot of the front. However, when an alongshore pressure gradient is added to simulate the observed mean southwestward flow along the northeast continental margin there is no reversal in the alongshore flow in the BBL under the front (see their Fig. 13). Thus our observations substantiate several important features of their frontogenesis model.

Since we are following the dye tagged water in a Lagrangian sense the observed cooling, dT/dt ~ 4x10^-6oC/s, must be the result of diffusive mixing. From the cross-shelf spreading of the dye patch we estimate a cross-shelf diffusivity of K_x ~ 10 m²/s. The cross-shelf variance of the dye patch increases approximately as time squared indicating a major contribution from shear dispersion. From measured cross-shelf temperature gradients an upper bound for T_xx is ~ 0.1x10-6^oC/m² so that the cross-shelf heat flux K_xT_xx ~ 1x10-6^oC/s. Since this is only one forth of dT/dt there must be significant vertical heat flux through the top of the BBL to achieve a local heat balance. An estimate of the vertical diffusivity K_z across the highly stratified top of the BBL is problematical but a value of K_z ~ 10^-5 m²/s yields K_zT_zz ~ 4x10^{-6 o}C/s which is approximately the magnitude required to account for the cooling of the dye patch. Using the same diffusivity results in a loss of approximately 1-3 l of dye which when subtracted from the 16 l initially injected into the BBL is consistent with the final dye inventory of 11.5 l. There is no evidence that double-diffusive mixing is a factor here. First, the density ratio,

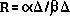is approximately 0.4 and not near unity where double diffusive processes are more active. Second, the T-S values of the water parcel evolves along the mean mixing curve between Shelf and Slope Water properties with no evidence of a counterclockwise rotation as modeled by Schmidt (1981). When warrented by better dye patch sampling in future experiments these flux calculations will be repeated by properly integrating over the entire patch rather than using mean patch values. However, even these crude estimates impose an upper bound on the diffusive flux through the highly stratified boundary of the BBL near the foot of the front.

If to some extent the structure depicted in Fig. 4 represents a steady-state condition in the coastal regime with no alongshore variation then both mass and heat balance must apply. Mass balance is probably achieved by an offshore flow confined to the stratified layer at the top of the BBL. Houghton et al. (1982) estimate that during the summer the 'cold pool', shelf water beneath the warm surface mixed layer, warms at approximately 1^oC /month. Approximating the cold pool as a wedge 100 km wide and 60m thick at the shelfbreak front this warming is equivalent to a heat flux of 4.9x106 W per meter of alongshelf distance. When mixed to 6^oC the onshore flow of 9^oC water in the BBL 6m thick at the measured speed of 0.015 m/s represents a flux of 1.1x106 W. Thus the heat flux associated with the onshore flow in the BBL at the foot of the front could contribute significantly to the Shelf Water heat balance and to exchange of Shelf and Slope Water properties via diapycnal mixing across the top of the BBL.

Lamont-Doherty Earth Observatory of Columbia University